SQL Server LOGITSUM Function
Updated 2024-02-13 20:13:13.277000
Description
Use the table-valued function LOGITSUM to calculate the binary logistic regression coefficients from a table of grouped x-values (the independent variables) with counts of the successes and failures for each group. The successes and failures can appear in any column and the column number of the successes and failures is specified at input.
| x1 | x2 | x3 | … | xn | success | failure |
|---|---|---|---|---|---|---|
| x 1,1 | x 1,2 | x 1,3 | … | x 1,n | success 1 | failure 1 |
| x 2,1 | x 2,2 | x 2,3 | … | x 2,n | success 2 | failure 2 |
| … | … | … | … | … | … | |
| x m,1 | x m,2 | x m,3 | … | x m,n | success m | failure m |
For dichotomous values, where the y-values are {0,1}, use the LOGIT function.
Logistic regression estimates the probability of an event occurring. Unlike ordinary least squares (see LINEST and LINEST_q) which estimates the value of a dependent variable based on the independent variables, LOGIT measures the probability (p) of an event occurring (1) or not occurring (0). The probability is estimated as:
p = \hat{\pi} = \frac{e^{\beta_0 + \beta_1x_1 + ... + ... \beta_nx_n}}{1 + e^{\beta_0 + \beta_1x_1 + ... + ... \beta_nx_n}}
The LOGIT function works by finding the coefficient (ß) values that maximize the log-likelihood statistic, which is defined as:
LL = \sum_{i=1}^n N_i \times \{y_i \times \ln \hat{\pi}(x_i) + (1 - y_i) \times \ln (1 - \hat{\pi}(x_i)\}
using a method of iteratively re-weighted least squares.
Syntax
SELECT * FROM [westclintech].[wct].[LOGITSUM](
<@Matrix_RangeQuery, nvarchar(max),>
,<@Success_ColumnNumber, int,>
,<@Failure_ColumnNumber, int,>)
Arguments
@Matrix_RangeQuery
the SELECT statement, as a string, which, when executed, creates the resultant table of x-values including the counts of successes and failures.
@Success_ColumnNumber
the number of the column in the resultant table returned by @Matrix_RangeQuery which contains the count of successes. @Success_ColumnNumber must be of the type int or of a type that implicitly converts to int.
@Failure_ColumnNumber
the number of the column in the resultant table returned by @Matrix_RangeQuery which contains the count of failures. @Failure_ColumnNumber must be of the type int or of a type that implicitly converts to int.
Return Type
table
| colName | colDatatype | colDesc |
|---|---|---|
| stat_name | nvarchar(4000) | Identifies the statistic being returned: b estimated coefficient for each independent variable plus the intercept se standard error of b z z statistic for b pval p-value (normal distribution) for the z statistic Wald Wald statistic LL0 log-likelihood with just the intercept and no other coefficients LLM model log-likelihood chisq chi squared statistic df degrees of freedom p_chisq p-value of the chi-squared statistic AIC Akaike information criterion BIC Bayesian information criterion Nobs number of observations rsql log-linear ratio R2 rsqcs Cox and Snell's R2 rsqn Nagelkerke's R2 D deviance Iterations number of iteration in iteratively re-weighted least squares Converged a bit value identifying whether a solution was found (1) or not (0) AUROC area under the ROC curve For more information on how these statistics are calculated see the LOGIT documentation. |
| idx | int | Identifies the subscript for the estimated coefficient (b), standard error of the coefficient (se), z statistics (z), p-value of the z statistic (pval), and the Wald statistic. When the idx is 0, it is referring to the intercept, otherwise the idx identifies the column number of independent variable. Descriptive statistics other than the ones mentioned above will have an idx of NULL. |
| stat_val | float | the calculated value of the statistic. |
Remarks
If @Success_ColumnNumber is NULL then the second right-most column in the resultant table is assumed to contain the count of successes.
If @Failure_ColumnNumber is NUL then the right-most column in the resultant table is assumed to contain the count of failures.
@Matrix_RangeQuery must return at least 3 columns or an error will be returned.
If @Success_ColumnNumber is not NULL and @Success_ColumnNumber < 1 an error will be returned.
If @Failure_ColumnNumber is not NULL and @Success_ColumnNumber < 1 an error will be returned.
If @Success_ColumnNumber is not NULL and @Success_ColumnNumber greater than the number of columns returned by @Matrix_RangeQuery an error will be returned.
If @Failure_ColumnNumber is not NULL and @Failure_ColumnNumber greater than the number of columns returned by @Matrix_RangeQuery an error will be returned.
Examples
Using the coronary heart disease data from LOGIT Example #1, we summarize the data into the 8 different age groups in Hosmer and use the summarized data in the logistic regression. This summarization can be handled entirely within the @MatrixRangeQuery string passed into the function.
SELECT *
INTO #chd
FROM ( VALUES (20, 0),
(23, 0),
(24, 0),
(25, 0),
(25, 1),
(26, 0),
(26, 0),
(28, 0),
(28, 0),
(29, 0),
(30, 0),
(30, 0),
(30, 0),
(30, 0),
(30, 0),
(30, 1),
(32, 0),
(32, 0),
(33, 0),
(33, 0),
(34, 0),
(34, 0),
(34, 1),
(34, 0),
(34, 0),
(35, 0),
(35, 0),
(36, 0),
(36, 1),
(36, 0),
(37, 0),
(37, 1),
(37, 0),
(38, 0),
(38, 0),
(39, 0),
(39, 1),
(40, 0),
(40, 1),
(41, 0),
(41, 0),
(42, 0),
(42, 0),
(42, 0),
(42, 1),
(43, 0),
(43, 0),
(43, 1),
(44, 0),
(44, 0),
(44, 1),
(44, 1),
(45, 0),
(45, 1),
(46, 0),
(46, 1),
(47, 0),
(47, 0),
(47, 1),
(48, 0),
(48, 1),
(48, 1),
(49, 0),
(49, 0),
(49, 1),
(50, 0),
(50, 1),
(51, 0),
(52, 0),
(52, 1),
(53, 1),
(53, 1),
(54, 1),
(55, 0),
(55, 1),
(55, 1),
(56, 1),
(56, 1),
(56, 1),
(57, 0),
(57, 0),
(57, 1),
(57, 1),
(57, 1),
(57, 1),
(58, 0),
(58, 1),
(58, 1),
(59, 1),
(59, 1),
(60, 0),
(60, 1),
(61, 1),
(62, 1),
(62, 1),
(63, 1),
(64, 0),
(64, 1),
(65, 1),
(69, 1)) n (age, chd)
SELECT *
FROM wct.LOGITSUM(
' SELECT a.age as [Age] ,SUM(c.chd) as Present ,COUNT(*) - SUM(c.chd) as Absent FROM #chd c CROSS APPLY ( SELECT TOP 1 age FROM (VALUES (20,1),(30,2),(35,3),(40,4) ,(45,5),(50,6),(55,7),(60,8) )n(age,grp) WHERE n.age <= c.age ORDER BY n.age DESC )a GROUP BY a.age',
2,
3)
This produces the following result.
| stat_name | idx | stat_val |
|---|---|---|
| b | 0 | -4.85868536330207 |
| b | 1 | 0.106379775834921 |
| se | 0 | 1.059814083208 |
| se | 1 | 0.0235010242724494 |
| z | 0 | -4.58446952185716 |
| z | 1 | 4.526601674959 |
| pval | 0 | 4.55140467350453E-06 |
| pval | 1 | 5.99397669650406E-06 |
| Wald | 0 | 21.0173607968372 |
| Wald | 1 | 20.4901227237416 |
| LL0 | NULL | -68.3314913574166 |
| LLM | NULL | -54.2283793396647 |
| chisq | NULL | 28.2062240355037 |
| df | NULL | 1 |
| p_chisq | NULL | 1.09053326927106E-07 |
| AIC | NULL | 112.456758679329 |
| BIC | NULL | 117.667099051306 |
| Nobs | NULL | 100 |
| rsql | NULL | 0.206392568603307 |
| rsqcs | NULL | 0.245773260267886 |
| rsqn | NULL | 0.32988140227239 |
| D | NULL | -0.462332717792356 |
| AUROC | NULL | 0.745818033455732 |
| Iterations | NULL | 5 |
| Converged | NULL | 1 |
As you can see the results are similar but not exactly the same as those produced using the raw data in LOGIT . Using the summarized data, the fitted values are given by the equation:
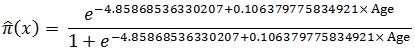
We can compare the results of the two models for a 60-year old using the following SQL.
SELECT 1 / (1 + EXP(-1 * (-5.30945337391905 + 0.1109211422069 * 60))) as P_raw,
1 / (1 + EXP(-1 * (-4.85868536330207 + 0.106379775834921 * 60))) as P_sum
This produces the following result.
| P_raw | P_sum |
|---|---|
| 0.793444615655287 | 0.821141607483233 |
Example #2
In this example we have 3 independent variables, a count of the number of successes and a count of the number of observations for each grouping. We will need to calculate the count of failures in @Matrix_RangeQuery .
SELECT *
INTO #t
FROM ( VALUES (100, 1, 10, 28, 156),
(150, 1, 10, 33, 144),
(200, 1, 10, 44, 171),
(250, 1, 10, 56, 196),
(300, 1, 10, 55, 158),
(350, 1, 10, 44, 100),
(400, 1, 10, 57, 126),
(450, 1, 10, 77, 166),
(500, 1, 10, 84, 166),
(100, 2, 10, 23, 153),
(150, 2, 10, 31, 165),
(200, 2, 10, 40, 179),
(250, 2, 10, 42, 152),
(300, 2, 10, 55, 181),
(350, 2, 10, 68, 200),
(400, 2, 10, 59, 148),
(450, 2, 10, 69, 156),
(500, 2, 10, 75, 157),
(100, 1, 11, 19, 164),
(150, 1, 11, 23, 147),
(200, 1, 11, 35, 182),
(250, 1, 11, 46, 196),
(300, 1, 11, 41, 143),
(350, 1, 11, 60, 189),
(400, 1, 11, 59, 162),
(450, 1, 11, 75, 187),
(500, 1, 11, 59, 129),
(100, 2, 11, 9, 105),
(150, 2, 11, 22, 179),
(200, 2, 11, 30, 182),
(250, 2, 11, 32, 155),
(300, 2, 11, 41, 164),
(350, 2, 11, 58, 200),
(400, 2, 11, 60, 181),
(450, 2, 11, 75, 199),
(500, 2, 11, 59, 141)) n (x1, x2, x3, success, N)
SELECT *
FROM wct.LOGITSUM('SELECT x1,x2,x3,success,n-success from #t', 4, 5)
This produces the following result.
| stat_name | idx | stat_val |
|---|---|---|
| b | 0 | 1.47313667574166 |
| b | 1 | 0.00420051489570411 |
| b | 2 | -0.169229814246798 |
| b | 3 | -0.323988399455435 |
| se | 0 | 0.628307634096669 |
| se | 1 | 0.000241365967082602 |
| se | 2 | 0.0589477537583747 |
| se | 3 | 0.0590000710920504 |
| z | 0 | 2.34461049937682 |
| z | 1 | 17.4030951690326 |
| z | 2 | -2.8708441536291 |
| z | 3 | -5.4913221875607 |
| pval | 0 | 0.0190469656457266 |
| pval | 1 | 7.81629936122213E-68 |
| pval | 2 | 0.00409377299880153 |
| pval | 3 | 3.98935835481458E-08 |
| Wald | 0 | 5.49719839378803 |
| Wald | 1 | 302.867721462405 |
| Wald | 2 | 8.24174615442641 |
| Wald | 3 | 30.1546193675964 |
| LL0 | NULL | -3573.5582397508 |
| LLM | NULL | -3396.62788760086 |
| chisq | NULL | 353.860704299878 |
| df | NULL | 3 |
| p_chisq | NULL | 2.17621977974947E-76 |
| AIC | NULL | 6801.25577520171 |
| BIC | NULL | 6827.97234303532 |
| Nobs | NULL | 5879 |
| rsql | NULL | 0.0495109748546528 |
| rsqcs | NULL | 0.0584149763613681 |
| rsqn | NULL | 0.083034978045949 |
| D | NULL | -0.101557327043684 |
| AUROC | NULL | 0.639751323614436 |
| Iterations | NULL | 4 |
| Converged | NULL | 1 |
See Also
LINEST - the Ordinary Least Squares (OLS) solution for a series of x-values and y-values
LOGEST - Logarithmic regression
LOGITPRED - Calculate predicted values based on a logit regression