SQL Server RANDLOGISTIC Function

Updated 2023-10-18 16:02:54.967000

Description

Use the table-valued function RANDLOGISTIC to generate a sequence of random numbers from a logistic distribution with parameters @Location and @Scale.

Syntax

SELECT * FROM [westclintech].[wct].[RANDLOGISTIC](
  <@Rows, int,>
 ,<@Location, float,>
 ,<@Scale, float,>)

Arguments

@Rows

the number of rows to generate. @Rows must be of the type int or of a type that implicitly converts to int.

@Location

the location parameter. @Shape must be of the type float or of a type that implicitly converts to float.

@Scale

the scale parameter. @Scale must be of the type float or of a type that implicitly converts to float.

Return Type

table

colName	colDatatype	colDesc
Seq	int	A monotonically increasing sequence number
X	float	The random variable

Remarks

@Scale must be greater than zero.

If @Shape is NULL then @Shape is set to 0.

If @Scale is NULL then @Scale is set to 1.

If @Rows is less than 1 then no rows are returned.

Examples

In this example we create a sequence of 1,000,000 random numbers rounded to one decimal place from the logistic distribution with @Location = 0 and @Scale =1, COUNT the results, and paste them into Excel, and graph them.

SELECT X,
       COUNT(*) as [COUNT]
FROM
(
    SELECT ROUND(X, 1) as X
    FROM wct.RANDLOGISTIC(   1000000, --@Rows
                             0,       --@Location
                             1        --@Scale
                         )
) n
GROUP BY X
ORDER BY X;

This produces the following result.

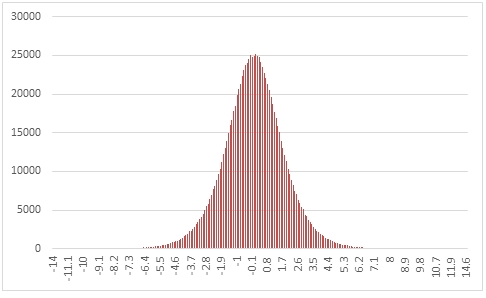
In this example we generate 1,000,000 random numbers from a logistic distribution with @Location of 60 and @Scale of 1.333333. We calculate the mean, standard deviation, skewness, and excess kurtosis from the resultant table and compare those values to the expected values for the distribution.

DECLARE @size as int = 1000000;
DECLARE @location as float = 60;
DECLARE @scale as float = 1.333333;
DECLARE @mean as float = @location;
DECLARE @var as float = POWER(@scale, 2) * POWER(PI(), 2) / 3e+00;
DECLARE @stdev as float = SQRT(@var);
DECLARE @skew as float = 0;
DECLARE @kurt as float = 1.2;
SELECT stat,
       [RANDLOGISTIC],
       [EXPECTED]
FROM
(
    SELECT x.*
    FROM
    (
        SELECT AVG(x) as mean_LOGISTIC,
               STDEVP(x) as stdev_LOGISTIC,
               wct.SKEWNESS_P(x) as skew_LOGISTIC,
               wct.KURTOSIS_P(x) as kurt_LOGISTIC
        FROM wct.RANDLOGISTIC(@size, @location, @scale)
    ) n
        CROSS APPLY
    (
        VALUES
            ('RANDLOGISTIC', 'avg', mean_LOGISTIC),
            ('RANDLOGISTIC', 'stdev', stdev_LOGISTIC),
            ('RANDLOGISTIC', 'skew', skew_LOGISTIC),
            ('RANDLOGISTIC', 'kurt', kurt_LOGISTIC),
            ('EXPECTED', 'avg', @mean),
            ('EXPECTED', 'stdev', @stdev),
            ('EXPECTED', 'skew', @skew),
            ('EXPECTED', 'kurt', @kurt)
    ) x (fn_name, stat, val_stat)
) d
PIVOT
(
    sum(val_stat)
    FOR fn_name in ([RANDLOGISTIC], [EXPECTED])
) P;

This produces the following result (your result will be different).

stat	RANDLOGISTIC	EXPECTED
avg	59.9999110998668	60
kurt	1.16521984825869	1.2
skew	-0.000310984734915708	0
stdev	2.41533527763239	2.4183985477125