SQL Server RANDBETA Function

Updated 2023-10-18 15:29:15.583000

Description

Use the table-valued function RANDBETA to generate q sequence of random numbers from the beta distribution with two positive shape parameters @a and @b.

Syntax

SELECT * FROM [westclintech].[wct].[RANDBETA](
  <@Rows, int,>
 ,<@a, float,>
 ,<@b, float,>)

Arguments

@Rows

the number of rows to generate. @Rows must be of the type int or of a type that implicitly converts to int.

@a

the first shape parameter. @a must be of the type float or of a type that implicitly converts to float.

@b

the second shape parameter. @b must be of the type float or of a type that implicitly converts to float.

Return Type

table

colName	colDatatype	colDesc
Seq	int	A monotonically increasing sequence number
X	float	The random variable

Remarks

@a must be greater than zero.

@b must be greater than zero.

If @a is NULL then @a is set to 1.

If @b is NULL then @b is set to 1.

If @Rows is less than 1 then no rows are returned.

Examples

In this example we create a sequence 1,000,000 random numbers rounded to two decimal places from a beta distribution with @a = 0.5 and @b = 0.5, COUNT the result, paste them into Excel and graph them.

SELECT X,
       COUNT(*) as [COUNT]
FROM
(
    SELECT ROUND(x, 2) as X
    FROM wct.RANDBETA(   1000000, --@Rows
                         0.5,     --@a
                         0.5      --@b
                     )
) n
GROUP BY X
ORDER BY 1;

This produces the following result.

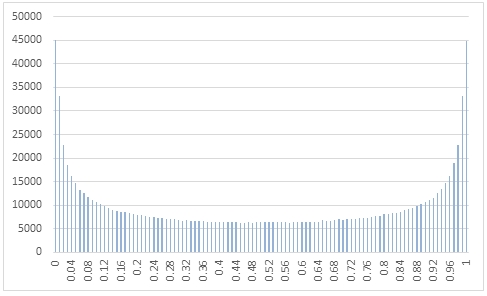
In this example we generate 1,000,000 random numbers from a beta distribution with @a of 2 and @b of 5. We calculate the mean, standard deviation, skewness, and excess kurtosis from the resultant table and compare those values to the expected values for the distribution.

DECLARE @size as int = 1000000;
DECLARE @a as float = 2;
DECLARE @b as float = 5;
DECLARE @mean as float = @a / (@a + @b);
DECLARE @var as float = (@a * @b) / (POWER(@a + @b, 2) * (@a + @b + 1));
DECLARE @stdev as float = SQRT(@var);
DECLARE @skew as float = (2 * (@b - @a) * SQRT(@a + @b + 1)) / ((@a + @b + 2) * 
          SQRT(@a * @b));
DECLARE @kurt as float
    = (6 * (POWER(@a - @b, 2) * (@a + @b + 1) - @a * @b * (@a + @b + 2))) / (@a * 
              @b * (@a + @b + 2) * (@a + @b + 3));
SELECT stat,
       [RANDBETA],
       [EXPECTED]
FROM
(
    SELECT x.*
    FROM
    (
        SELECT AVG(x) as mean_BETA,
               STDEVP(x) as stdev_BETA,
               wct.SKEWNESS_P(x) as skew_BETA,
               wct.KURTOSIS_P(x) as kurt_BETA
        FROM wct.RANDBETA(@size, @a, @b)
    ) n
        CROSS APPLY
    (
        VALUES
            ('RANDBETA', 'avg', mean_BETA),
            ('RANDBETA', 'stdev', stdev_BETA),
            ('RANDBETA', 'skew', skew_BETA),
            ('RANDBETA', 'kurt', kurt_BETA),
            ('EXPECTED', 'avg', @mean),
            ('EXPECTED', 'stdev', @stdev),
            ('EXPECTED', 'skew', @skew),
            ('EXPECTED', 'kurt', @kurt)
    ) x (fn_name, stat, val_stat)
) d
PIVOT
(
    sum(val_stat)
    FOR fn_name in ([RANDBETA], [EXPECTED])
) P;

This produces the following result (your result will be different).

stat	RANDBETA	EXPECTED
avg	0.28577495782875	0.285714285714286
kurt	-0.119163723672499	-0.12
skew	0.597784901594543	0.596284793999944
stdev	0.159684726349007	0.159719141249985